Table of Contents
When Gaussian Process Meets Big Data: A Review of Scalable GPs
liu_when_2020
Haitao Liu, Yew-Soon Ong, Xiaobo Shen, and Jianfei Cai, “When Gaussian Process Meets Big Data: A Review of Scalable GPs”, IEEE Transactions on Neural Networks and Learning Systems, vol. 31, Nov. 2020, pp. 4405–4423.
Terms and Acronyms
| Acronyms | Full terms | Notes |
| FITC | fully independent training conditional | |
| FIC | fully independent conditional | |
| PITC | partially independent training conditional | |
| PIC | partially independent conditional | |
| DTC | deterministic training conditional | |
| SoR | subset of data | |
| MVM | Matrix-Vector Multiplications | [1] |
| SVI | Stochastic Variational Inference | |
| MoE | Mixture of Experts | |
| PoE | Product of Experts | |
| LVM | Latent variable model |
VII. CONCLUSION
Although the GP itself has a long history, the nonparametric flexibility and the high interpretability make it popular yet posing many challenges in the era of big data. In this article, we have attempted to summarize the state of scalable GPs in order to well understand the state of the art and attain insights into new problems and discoveries. The extensive review seeks to uncover the applicability of scalable GPs to real-world large-scale tasks, which in turn present new challenges, models, and theory in the GP community.
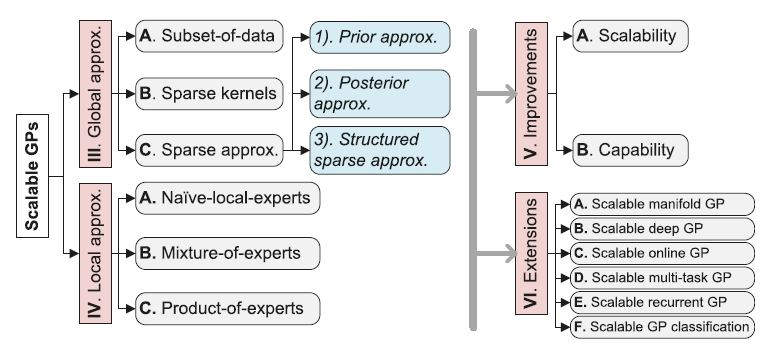
I. INTRODUCTION
Global Approximations: It approximates the kernel matrix $K_{nn}$ through global distillation.
Local Approximations: It follows the divide-and-conquer (D&C) idea to focus on the local subsets of training data. Efficiently, local approximations only need to tackle a local expert with $m_0 (m_0 \ll n)$ data points at each time [19], [20]. In addition, to produce smooth predictions equipped with valid uncertainty, modeling averaging has been employed through mixture or product of experts [21]–[28].
II. GP REGRESSION REVISITED
The computational bottleneck in (2) is solving the linear system $(K_{nn}^\epsilon)^{-1} \mathbf{y}$ and the determinant $|K_{nn}^\epsilon|$.
IV. LOCAL APPROXIMATIONS
A. Naive Local Experts
To address the generalization issue, it is possible to
1) share the hyperparameters across experts, such as [26]; or
2) combine local approximations with global approximations, which will be reviewed in Section V-B.
B. Mixture of Experts
MoE generally expresses the combination as a Gaussian mixture model (GMM) [120].
The training of MoE usually assumes that the data are i.i.d. such that we maximize the factorized log likelihood to learn the gating functions and the experts simultaneously by the gradient-based optimizers [124] and, more popularly, the EM algorithm [120], [122], [125], [126]. The joint learning permits probabilistic (soft) partition of the input space via both the data and the experts themselves, and diverse experts specified for different but overlapped subregions.
The mixture of GP experts for big data should address two issues:
1) how to reduce the computational complexity (model complexity) and
2) how to determine the number of experts (model selection).
To address the model complexity issue, there are three core threads.
The first is the localization of experts.
The second thread is to combine global experts with the sparse approximations reviewed in Section III-C under the variational EM framework.
To relieve the problem of MILE, the third thread is to prepartition the input space by clustering techniques and assign points to the experts before training [138], [139].
Finally, to address the model selection issue, the Akaike information criterion [140] and the synchronously balancing criterion [141] have been employed to choose over a set of candidate M values.
C. Product of Experts
整体来看PoE问题很多,衍生方法也很多。
V. IMPROVEMENTS OVER SCALABLE GPs
A. Scalability
B. Capability
Hence, in order to enhance the representational capability of scalable GPs, the hybrid approximations are a straightforward thread by combining global and local approximations in tandem.
后续需要重点看这部分的文献
Alternatively, the hybrid approximations can be accomplished through an additive process [41], [163], [164]. For instance, after partitioning the input space into subregions, the PIC [41] and its stochastic and distributed variants [35], [43], [87] extend PITC by retaining the conditional independence of training and test, …, for all the subregions except for the one containing the test point $x_*$. Thus, it enables the integration of local and global approximations in a transductive pattern. Mathematically, suppose that $x_* \in \Omega_j$ , and we have $$ q(\mathbf{f}, f_* | \mathbf{f}_m) = p(\mathbf{f}_j, f_* | \mathbf{f}_m) \Pi_{i\neq j}^M p(\mathbf{f}_j | \mathbf{f}_m) \tag{30} $$ This model corresponds to an exact GP with an additive kernel $$ k_\text{PIC}(\mathbf{x}_i, \mathbf{x}_j) = k_\text{SoR}(\mathbf{x}_i, \mathbf{x}_j) + \psi_{ij} [ k(\mathbf{x}_i, \mathbf{x}_j) - k_\text{SoR}(\mathbf{x}_i, \mathbf{x}_j) ] $$
The additive kernel similar to $k_\text{PIC}$ has also been employed in [163]–[165] by combining the CS kernel [15], [52] and the sparse approximation. Furthermore, as an extension of PIC, the tree-structured GP [166] [2] ignores most of the intersubregion dependences of inducing points, but it concentrates on the dependence of the adjacent subregions lying on a chained tree structure. The almost purely localized model reduces the time complexity to be linear to $n$ and allows using many inducing points.
Park and Choi [167] [ref167_park_hierarchical_2010] presented a two-layer model, in which a GP is placed over the centroids of the subsets as $g(c) \sim \mathcal{GP}(0, k_g(\mathbf{c}, \mathbf{c}'))$ to construct a rough global approximation in the top layer; then in each subregion of the root layer, a local GP is trained by using the global-level GP as the mean prior $f_i(x) \sim \mathcal{GP}(g(x), k_ii(\mathbf{x}, \mathbf{x}'))$. This model has also been improved into multilayer structure [168] [3] .
The PIC predictive distribution is composed of both global and local terms [41], which partially alleviate the discontinuity. To completely address the discontinuity, Nguyen and Bonilla [42] [5] and Nguyen et al. [133] [6] combined sparse approximations with model averaging strategies, e.g., MoE.
VI. EXTENSIONS AND OPEN ISSUES
D. Scalable Online GP
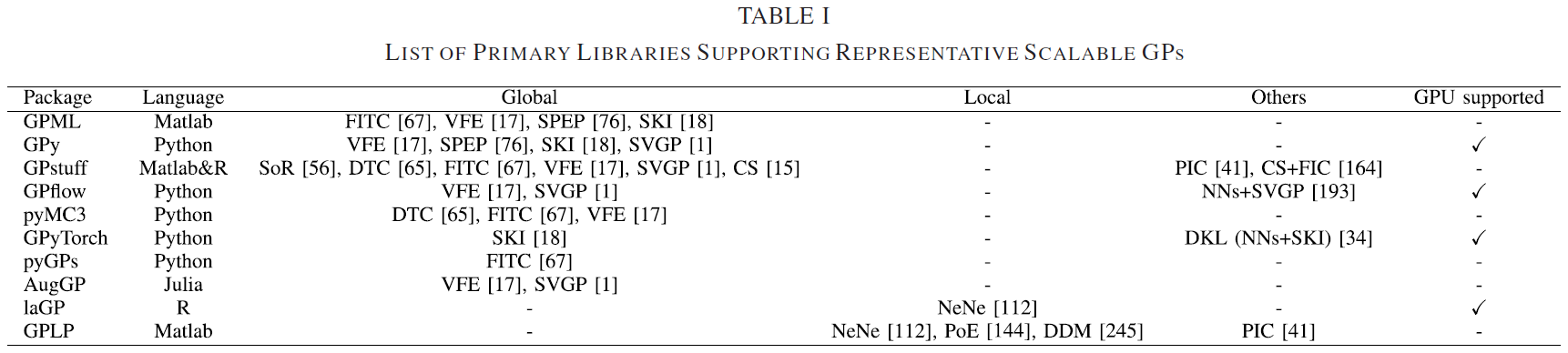
Sparse GPs are extensible for online learning since they employ a small inducing set to summarize the whole training data [210]–[212]. As a result, the arrived new data only interact with the inducing points to enhance fast online learning. This is reasonable since the updates of $\mu(\mathbf{x}_*)$ and $\sigma^2(\mathbf{x}_*)$ of FITC and PITC only rely on the inducing set and new data [213], [214]. Moreover, the stochastic variants naturally showcase the online structure [215], since the bound in (17) supports minibatch learning by stochastic optimization.
there are two issues for scalable online GPs.
First, some of them [211], [213], [214] fix the hyperparameters to obtain constant complexity per update. It is empirically argued that the optimization improves the model significantly in the first few iterations [215]. Hence, with the advanced computing power and the demand for accurate predictions, it could update the hyperparameters online over a small number of iterations.
Second, the scalable online GPs implicitly assume that the new data and the old data are drawn from the same input distribution.
To address the evolving online learning, Nguyen et al. [217] [7] presented a simple and intuitive idea using local approximations. This method maintains multiple local GPs and either uses the new data to update the specific GP when they fall into the relevant local region or uses the new data to train a new local GP when they are far away from the old data, resulting in, however, information loss from available training data. (后续重点以为这篇为基础)