Table of Contents
Nonmyopic active learning of Gaussian processes: an exploration-exploitation approach
我主要是看这篇文章中的 nonstationary GP model,因为在另一篇文章 Bayesian optimization with adaptive kernels for robot control 中对这篇进行了重点引用。
krause_nonmyopic_2007
Andreas Krause, and Carlos Guestrin, “Nonmyopic active learning of Gaussian processes: an exploration-exploitation approach”, Proceedings of the 24th international conference on Machine learning, New York, NY, USA: Association for Computing Machinery, 2007, pp. 449–456. Link.
A fundamental question is when an active learning, or sequential design, strategy, where locations are selected based on previous measurements, will perform significantly better than sensing at an a priori specified set of locations.
Central to our analysis is a theoretical bound which quantifies the performance difference between active and a priori design strategies. We consider GPs with unknown kernel parameters and present a nonmyopic approach for trading off exploration, i.e., decreasing uncertainty about the model parameters, and exploitation, i.e., near-optimally selecting observations when the parameters are (approximately) known.
We then extend our algorithm to handle nonstationary GPs exploiting local structure in the model. (这里才涉及到了不同kernel的组合)
Introduction
Most approaches for active sampling of GPs have been myopic in nature, in each step selecting observations which, e.g., most decrease the predictive variance. Our approach however is nonmyopic in nature: we prove logarithmic sample complexity bounds on the duration of the exploration phase, and near optimal performance in the exploitation phase.
nonstationary processes are often defined by a much larger number of parameters. To address this issue, we extend our algorithm to handle nonstationary GPs with local structure, providing efficient exploration strategies and computational techniques that handle high dimensional parameter vectors.
2. Gaussian Processes
In Section 3, we address a general form (not necessarily isotropic), where the kernel function is specified by a set of parameters $\theta$. We adopt a hierarchical Bayesian approach and assign a prior $P(\theta)$ to the parameters $\theta$, which we assume to be discretized in our analysis.
3. Observation Selection Policies
Entropy. The entropy criterion has been frequently used to select observations in GPs (c.f., Seo et al. (2000); Shewry and Wynn (1987)). Here, we select observations $\mathcal{A}^*\subseteq\mathcal{V}$ with highest entropy: $$ \mathcal{A}^* = \text{argmax}_{\mathcal{A}\subseteq\mathcal{V}} H(\mathcal{X}_\mathcal{A}) \tag{3.1}$$ where $H(\mathcal{X}_\mathcal{A}) = - \int p(x_\mathcal{A}) \log p(x_\mathcal{A}) dx_\mathcal{A}$ is the joint (differential) entropy of the random variables $\mathcal{X}_\mathcal{A}$. 看不懂
Caselton and Zidek (1984) proposed the mutual information criterion for observation selection, $\text{MI}(\mathcal{X}_\mathcal{A}) = H(\mathcal{X}_{\mathcal{V}\backslash\mathcal{A}}) − H(\mathcal{X}_{\mathcal{V}\backslash\mathcal{A}} | \mathcal{X}_\mathcal{A})$. 看不懂 Guestrin et al. (2005) showed that this criterion selects locations which most effectively reduce the uncertainty at the unobserved locations, hence it often leads to better predictions compared to the entropy criterion.
A natural generalization of mutual information to the sequential setting is…
The greedy policy $\pi_\text{IE}$ for mutual information
4. Bounds on the Advantage of Active Learning Strategies
If the GP parameters $\theta$ are known, it holds that…
…
Thus, the entropy of a set of variables does not depend on the observed values $x_\mathcal{A}$.
…
More generally, any objective function depending only on the predictive variances, such as mutual information, cannot benefit from sequential strategies.
确定参数的GP无法通过sequential受益。
Note that for non-Gaussian models, sequential strategies can strictly outperform a priori designs, even with known parameters.
确定参数的GP无法通过sequential受益。
In the case of GPs with unknown parameters,
…
The following central result formalizes this intuition, by bounding $H(\mathcal{X}_\pi)$ (and similarly for mutual information) of the optimal policy $\pi$ by a mixture of entropies of sets $H(\mathcal{X}_\mathcal{A} | \theta)$, which are chosen optimally for each fixed parameter (and can thus be selected a priori):
…
Theorem 1.
…
This result implies, that if we are able to (approximately) find the best set of observations $A_{\theta}$ for a GP with known parameters $\theta$, we can bound the advantage of using a sequential design. If this advantage is small, we select the set of observations ahead of time, without having to wait for the measurements.
5. Exploration–Exploitation Approach towards Learning GPs
6. Actively Learning Nonstationary GPs
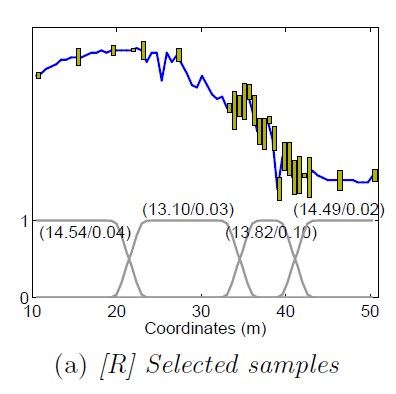
In our river example, we set the weighting functions as indicated in Figure 2(a).
6.2 Efficient Nonstationary Active Learning
Andreas Krause, and Carlos Guestrin, Nonmyopic Active Learning of Gaussian Processes: An Exploration-Exploitation Approach, Pittsburgh PA 15213: Carnegie Mellon University, 2007. Link.
这里的简单情况,一个点属于一个GP,类似于 Nguyen-Tuong et al. [1] 使用的模型。
8. Related Work
Gramacy (2005) presents a nonstationary, hierarchical Bayesian GP approach based on spatial partitioning, where the spatial decomposition is integrated out using MCMC methods, which however does not provide any theoretical performance guarantee.
9. Conclusions
Here, we used a variational approach to address the combinatorial growth of the parameter space.