Two-line Element

NORAD ID finder:

• https://celestrak.com/satcat/search.php
• https://www.n2yo.com/database/
• Or, just google satellite-name NORAD ID

TLE sets download:

• https://www.space-track.org/ (direct download, real-time, account required)
• https://www.celestrak.com/NORAD/archives/request.php (archived data, request and then retrieve by email)

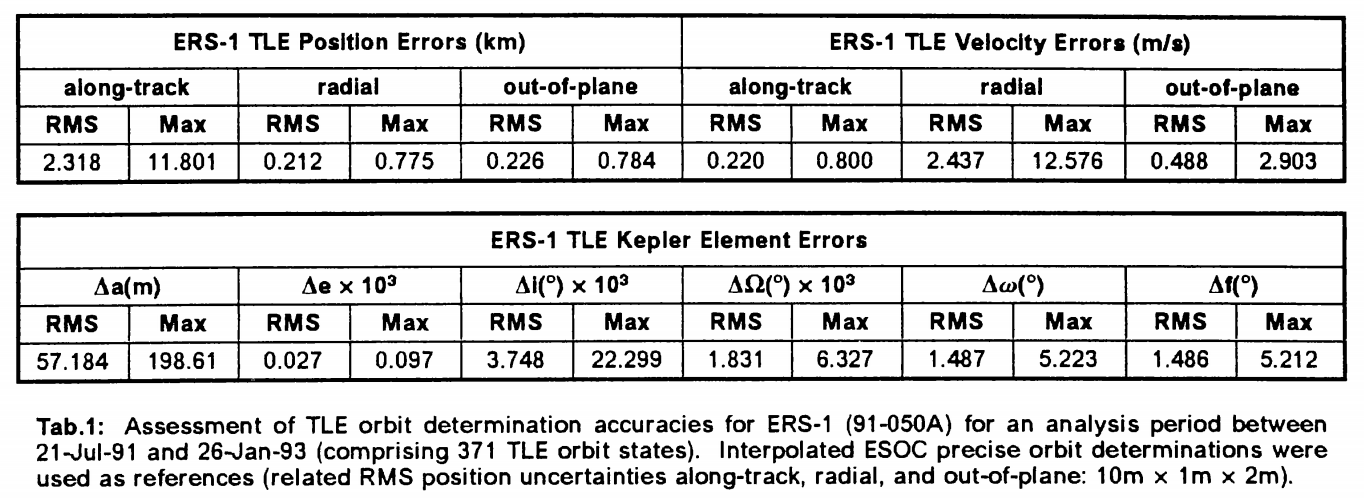
A TLE assessment result of ERS-1 using high accuracy OD results, from H. Klinkrad [1] in 1997.

在后续的conjunction analysis计算中，对所有其它RSO，使用ERS-1的 1-sigma Kepler element uncertainties的120%倍做计算，bstar取本身的10%作为1-sigma。

When assessing ERS-1 and ERS-2 conjunction events with catalog objects it shall be assumed that both ERS spacecraft have TLE orbit determination errors corresponding to the 1u Kepler element uncertainties listed in Tab.1, and that ballistic parameter information (i.e. the TLE quantity n/2) has a 1u uncertainty corresponding to 10% of its magnitude. For the chaser objects a 20% larger rms error shall be adopted for the same parameter set. [1]

把 single TLE set 向前后向积分一圈，然后和高精度轨道数据对比，把得到是 RMS 当作 initial uncertainty covariance。

In PROXIM-A the TLE covariance is estimated by analytical propagation of an initial error covariance matrix derived for ERS-1 by comparison of ESOC precise orbit data with corresponding TLE predictions over $\pm1$ revolution about TLE epoch. [1]

COVGEN is the standard one.

Their method started with a pair-wise differencing of a set of TLEs for a 14-day time span, then computed residuals (observed – calculated measurements) in a satellitebased coordinate system, performed a quadratic least squares fit, calculated a standard deviation from those, and removed outliers (TLEs beyond 3-sigma). They then calculated a second best fit of the remaining residuals, and used that as the time-varying error estimation.

The error at epoch for LEO satellites were determined by calculating the root-sum-square (RSS) of the observations in each component over the first 1.5 days (16:203). For higher altitude objects, they directly compared each SGP4 TLE to a high-precision state vector available from a commercial source. [2]

ESA's European Space Operations Centre (ESOC) has several conjunction analysis tools in use:

• Computation of Miss distance Between Objects (COMBO)
• Collision Analysis for Launcher Ascent Trajectories (COLA)
• (PROXIM-A)
• Collision Risk Assessment Tool (CRASS)

Interpolation techniques are used for the available orbit files, while the remaining orbits have to be propagated with the SGP-4/SDP-4 theory.

CRASS finally uses Akella and Alfriend's algorithm [4] to calculate the collision risk.